Եկեք մի փոքրիկ վարժություն անենք։ Եթե պատուհանի մոտ լուսամփոփ տեղադրենք, նստենք հստակ մի դիրքում և նայենք սկզբում ձախ աչքով, ապա՝ աջ աչքով, կնկատենք, որ լուսամփոփի դիրքը փոփոխվում է պատուհանի նկատմամբ։ Չնայած լուսամփոփը մնում է նույն դիրքում, մեր աչքերը գտնվում են իրարից մի քանի սանտիմետր հեռավորության վրա, և կախված աչքի դիրքից, լուսամփոփը մեր նկատմամբ փոխում է իր դիրքը:

Իհարկե լուսամփոփի փոխարեն կարող է լինել ցանկացած առարկա, նույնիսկ կարող եք ձեր մատը պարզել և մեկ աջ աչքով նայել, մեկ՝ ձախ։ Այս երևույթը անվանում են պարալաքս: Ինչքան մոտ է առարկան, այնքան ավելի մեծ է տեղաշարժը։ Սա ճիշտ է նաև աստղագիտության պարագայում, այսինքն շատ ավելի մեծ մասշտաբների դեպքում։
Պարալաքսը տիեզերական հեռավորությունների համար:
Մեր աչքը սկսում է պարալաքսի էֆֆեկտը չզգալ, երբ առարկաները մեզանից մոտ 1.4կմ-ից ավելի հեռու են: Երկրագնդից նայելիս տիեզերքը երկչափ է թվում, և անհնար է աչքով ասել, թե որ աստղը որքան է հեռու։ Մենք տեսնում ենք հազարավոր պայծառ կետեր, որոնք կարծես սև հարթության վրա սփռված լինեն, սակայն տիեզերքը, իհարկե, եռաչափ (կամ քառաչափ եթե ժամանակը նույնպես հաշվի առնենք), հսկայական՝ կարելի է ասել անսահման տարածություն է, որտեղ աստղերի հեռավորությունները շատ տարբեր են։ Սակայն աստղագետները հարյուրամյակներ են ծախսել հաշվարկելու համար, թե ինչպես են դասավորված և սփռված աստղերն ու այլ տիեզերական մարմինները տարածության մեջ։ Այս եռաչափ տիեզերական քարտեզի ստեղծման մեջ առաջին քայլը դեպի աստղերն ընկած հեռավորությունը չափելն է։
Աստղերի՝ երկրագնդից ունեցած հեռավորությունը գտնելու համար կա մի քանի հնարավոր տեխնիկա, որոնք օգտագործվում են զուգահեռաբար՝ ըստ հարմարության։ Նման ամենահայտնի մեթոդների մասին կխոսենք առաջիկա մի քանի նյութերի ընթացքում։ Երբ աստղերը գտնվում են Երկրագնդից մինչև 600 լուսատարի հեռավորության վրա, մենք կարող ենք նկատել, դրանց դիրքի տեղափոխությունն արևի շուրջը պտտվելու ընթացքում, այսպիսով հեռավորության չափման ամենահաճախ օգտագործվող մեթոդը պարալաքսի մեթոդն է, որի մասին կխոսենք այս բլոգում։
Պարալաքսի մեթոդը օգտագործում է երկու առարկաների միմյանց նկատմամբ շարժումը, որպեսզի հաշվարկի հեռավորությունը մինչ այդ առարկաները։
Պարալաքսի բանաձևն ասում է, որ դեպի աստղ հեռավորությունը հավասար է 1-ը բաժանած պարալաքսի անկյանը, որի դուրս բերումն ու մանրամասն քննարկումը ներկայացված է ներքևում։ Բանաձևը հարմար օգտագործելու համար, պարալաքսի անկյան չափման միավոր օգտագործում են վայրկյաններ (այստեղ այն ժամանակը ցույց չի տալիս, այլ անկյունը, և կազմում է մեկ աստիճանի 3600-րդ մասը), իսկ հեռավորության համար կօգտագործենք պարսեկները (այն հեռավորությունը, որը լույսն անցնում է մոտ 3.2 տարում)։
Պարալքսի բանաձը
Եկեք փորձենք կիրառել պարալաքսի էֆֆեկտը որևէ աստղի համար, չվախենաք ներքևի բանաձևերից, մենք մանրամասն կբացատրենք դրանք։


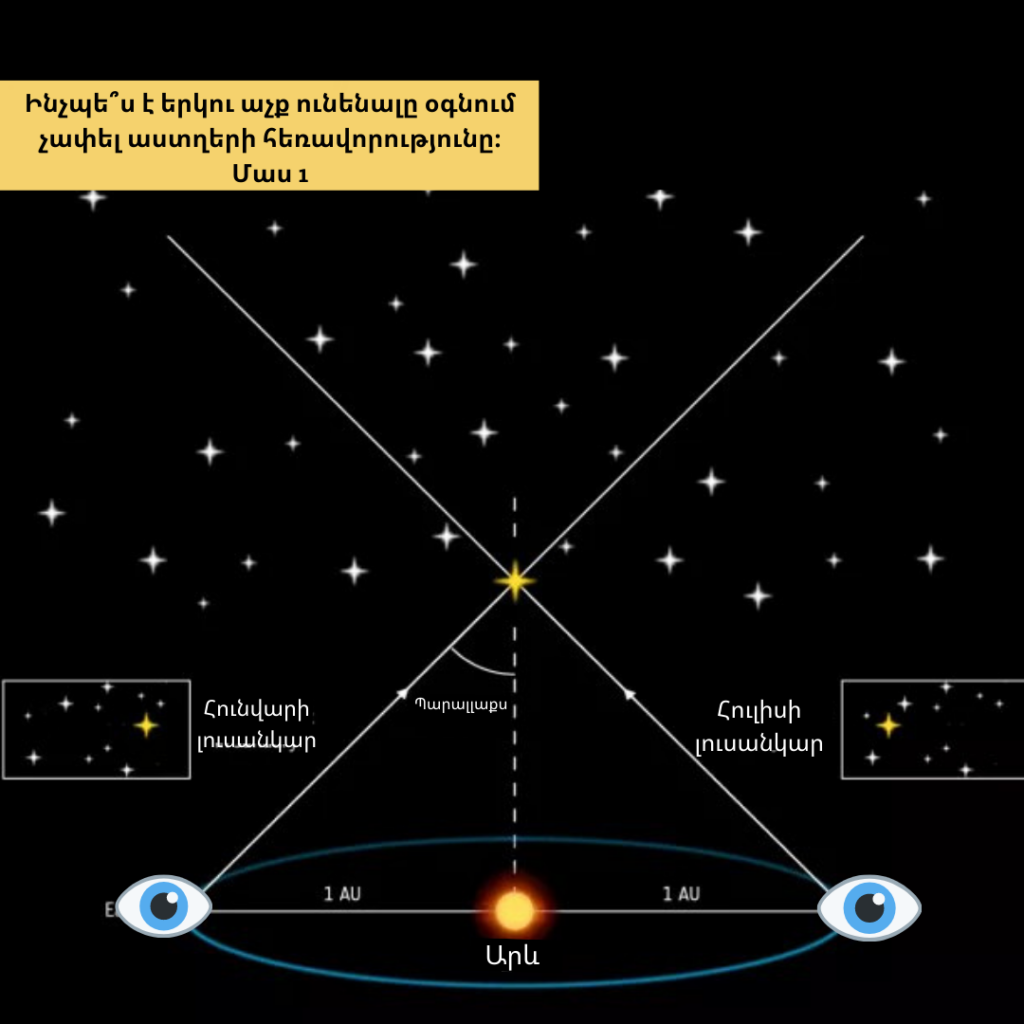
Աստղագիտական հեռավորությունները չափելու համար մեզ պետք կգա ունենալ «աչքեր» որոնցով երկու անգամ կնայենք նույն աստղին, ինչպես նայում էինք լուսամփոփին, սակայն յուրաքանչյուրը ուղեծրի հակառակ ծայրից (այսինքն մի չափումը մյուսից 6 ամիս անց)։ Այդպիսով երկու դիրքերի միջև հեռավորությունը ուղիղ 2 աստղագիտական միավոր (Երկիր-Արև հեռավորություն) կկազմի։ Երկրագնդի կատարած շարժումը համեմատած Արևի և աստղի հարաբերական շարժմանը հսկայական է, ինչի շնորհիվ էլ, ինչպես ներկայացված է նկ. 3-ում, աստղի և Արևի դիրքերը համարում ենք անփոփոխ։
Իսկ աստղի տեղափոխությունը մենք դիտարկում ենք այն աստղերի ֆոնի վրա, որոնք համեմատականորեն չեն փոխում իրենց դիրքը (դրանք շատ հեռու աստղեր են՝ տես նկ 2):

Երկրագնդի այս տեղափոխությունը բավարար է երկու դիրքերի միջև α անկյունը չափելի դարձնելու համար։ Վերևում ներկայացված գծագրում երևում է, որ երբ α անկյունը բաժանում ենք երկու մասի, ուղղանկյուն եռանկյուն ենք ստանում, որտեղ մի էջը Արևի ու մեզ հետաքրքրող աստղի հեռավորությունն է։ Նշանակենք p տառով α/2 անկյունը և անվանենք դա պարալաքսի անկյուն:

Ուղղանկյուն եռանկյան մեջ, անկյան տանգենս են անվանում դիմացի էջի հարաբերությունը կից էջին (նկ 4)։ Տանգենսի ֆունկցիան օգտագործելով, վերը ներկայացված գծագրում ուղղանկյուն եռանկյան համար, գտնում ենք աստղի հեռավորությունը․
tg(p)=1ԱՄ/d
Քանի որ աստղը գտնվում է հսկայական հեռավորության վրա, մենք կարող ենք օգտագործել այսպիսի մոտարկում, ըստ որի փոքր անկյունների տանգենսը գրեթե հավասար է այդ անկյանը։ Սա պարզեցնում է պարալաքսի բանաձևը դարձնելով՝ p=1ԱՄ/d, կամ, որ նույնն է՝
d=1ԱՄ/p
Աստղագիտական միավորը, սակայն, չափման ամենահարմար համակարգը չէ, և պարսեկների օգտագործումը տվյալ իրավիճակում նույնիսկ ավելի է պարզեցնում բանաձևը։ Պարսեկը սահմանված է որպես այն հեռավորություն, որը առաջանում է 1 վայրկյան (
աստիճանի 3600-րդ մասը) պարալաքս անկյան դեպքում 1ԱՄ հեռավորությունից նայելիս, այն մոտավորապես ստացվում է 3.26 լուսատարի կամ 206,000ԱՄ։ Այպիսով պարալաքսի բանաձևը կարող ենք գրել այսպես․
d=1/p պարսեկ ,
որտեղ p-ի չափման միավորը վայրկյանն է։
Փաստորեն ստացանք աստղի հեռավորությունը չափելու պարզ բանաձև` աստղի, Արեգակից ունեցած հեռավորությունը՝ արտահայտված պարսեկներով, հակադարձ համեմատական է պարալաքսի անկյանը: Այսինքն ինչքան մեծ է պարալաքսի անկյունը, այնքան մոտ է աստղը, և հակառակը:
Չափման մեծ ճշգրտության համար, իհարկե, անհրաժեշտ են մեծ ճշգրտության աստղադիտակներ, քանի որ պարալաքսի անկյունը շատ փոքր է: Արևին ամենամոտ գտնվող աստղը, և ուրեմն նաև աստղը, որն ունի ամենամեծ պարալաքսը՝ Պրոքսիմա Ցենտավրն է։ Դրա պարալաքսը 0.7685 ± 0.0002 վայրկյան է։ Այս ակյունը մոտավորապես համապատասխան է 2սմ տրամագծով, 5,3կմ հեռավորության վրա գտնվող մարմնի պարալաքսին:
Առաջին անգամ այս մեթոդի օգնությամբ հեռավորությունների հաշվարկներ արել է Ֆրիդրիխ Բեսսելը, 1838 թվականին։ Պարալքսի մեծամասշտաբ օգտագործումը սկսել է 1896ից, երբ Վիեննայում՝ Կաֆֆների աստղադիտարանում տեղադրվել է առաջին հելիոմետրը։ Հելիոմետրի սկզբնական կիրառումը եղել է արևի տրամագծի չափումը: Սարքը նման է սովորական աստղադիտակի պարզապես օկուլյարիոսպնյակը բաժանված է մեջտեղից երկու մասի, որոնցից մեկը շարժական է, մյուսը՝ անշարժ, այդ ձևով ստացվում է երկու պատկերներ, որոնք կարելի է շարժելով իրար վրա բերել, կամ հեռացնել իրարից: Հեռացնելով իրարից պատկերները, այնպես, որ առաջին պատկերը հազիվ դիպչում է երկրոդին, և չափելով տեղաշարժի չափը (միկրոմետրով) կիմանանք, թե որքան է Արևի տրամագիծը։ Նման ձևով նաև կարելի է չափել աստղի դիրքի փոփոխությունը մյուս աստղերի նկատմամբ:
Օգտագործելով իրարից մի քանի ժամ հետո արված լուսանկարներ, կարելի է նույնսիկ չափել դեպի Լուսին ընկած հեռավորությունը։ Մեր նկատմամբ Լուսնի դիրքի փոփոխությունը թույլ կտա գտնել պարալաքսը, այդպիսով նաև դեպի Լուսին հեռավորությունը։
Այլ կիրառություններ. որոշենք ծառի հեռավորությունը
Եթե մինչև այստեղ կարդացիք, ապա ձեզ առաջարկում ենք դա ստուգել պարալաքսի մեթոդը: Դրա համար կարող եք ինքներդ գծագրել և փորձեր իրականացնել հեռավոր մարմինների հեռավորությունները չափելու համար։ Պարալաքսի մեթոդը օգտագործում են ոչ միայն աստղերի հեռավորությունը չափելու համար, այլ նաև ամենօրյա իրավիճակներում, օրինակ մինչև մոտակա ծառի հեռավորությունը չափելու համար։
Եկեք չափենք ծառի հեռավորությունը, որը երևում է ավտոմեքենայով շարժվելիս, և գտնվում է սարի դիմաց: Նորից վերադառնալով լուսամփոփի փորձին, երկու տարբեր դիրքերից, սարի դիրքը լեռան նկատմամբ փոփոխվում է։ Մենք չենք նկատում լեռան դիրքի փոփոխությունը կարճ ճանապարհ գնալիս, բայց ակնհայտորեն տեսնում ենք ծառի դիրքի փոփոխությունը լեռան նկատմամբ։

Փորձը սկսենք այսպես, անկյունաչափով չափենք մեր դիրքից սարի գագաթի և ծառի կազմած անկյունը, նշանակենք դա A տառով, ապա շարժվենք ճանապարհով՝ անցնելով D ոչ մեծ հեռավորություն: Նույն գործողությունը անենք նաև այդտեղ, նշանակենք սարի գագաթի և ծառի կազմած անկյունը B տառով: Նկատենք, որ այստեղ մեր պարալաքսի անկյունը A և B անկյունների գումարն է, քանի որ մեր տեղափոխությունը քիչ է, և սարը այդ ընթացքում չնչին է տեղաշարժվում մեր տեսանկյունից: Օգտագործելով պարալաքսի մեթոդը՝ կարող ենք պարզապես գրել, որ մեքենայի երկու դիրքերի միջև D հեռավորության և ծառի R հեռավորությանը հարաբերությունը հավասար է A և B անկյունների գումարի տանգենսին։
R=D/tan((A+B))
Հավասարման միակ անհայտը ծառի հեռավորությունն է, որը հնարավորություն կտա սովորական հաշվիչի միջոցով գտնել այն։ Միգուցե հաջորդ անգամ Արագածի լանջին հասնելու ճանապարհին փորձե՞ք։ Գրեք մեկնաբանություններում ձեր արած փորձերի արդյունքները: